Dalam Statistik kita akan mempelajari yang namanya ukuran pusat data??
Apa saja ci yang termasuk dalam ukuran pusat data itu? ternyata dalam ukuran pusat data terdapat 3 cara penghitungan yang seringkali digunakan dalam statistik. Ada yang tau? yup, diantaranya pasti ada yang tau namanya:
* Mean : nilai rata-rata dimana rumus nya jumlah data dibagi dengan banyaknya data atau lebih lngkapnya
Rata-rata (mean) adalah hasil penjumlahan nilai-nilai anggota sebuah kelompok (∑Xn) dibagi jumlah anggota kelompok tersebut. Ada tiga jenis rata-rata yang dikenal dalam statistik yaitu rata-rata hitung (x ̅), rata-rata ukur (Gm atau U) dan rata-rata harmonik (rh atau H). adapun kegunaan dari rata-rata di atas sebagai berikut:
rata-rata hitung: Mengukur nilai rata-rata sebenarnya dari data misalnya Rata-rata nilai mata kuliah statistika untuk siswa MTs Darul Hikmah, Rata-rata jumlah pencari kerja selama tahun 1990 sampai 2004 yang terdaftat di Disnaker Surabaya
rata-rata ukur: Mengukur tingkat perubahan ( rate of change) untuk data nilai positif misalnya Rata-rata tingkat pertambahan pinjaman setiap bulan di kantor penggadaian. Diketahui data sambungan telpon selama setahun. Berapa rata-rata pertumbuhan sambungan telpon setiap bulan.
rata-rata harmonik: Mengukur nilai rata-rata data yang memiliki nilai positif dan ada rasio. Misalnya Tiga pegawai bagian pembelian diberi tugas membeli kayu di pedalaman. Setiap pegawai mendapat uang Rp. 450 juta. Dari hasil pembelian diperoleh bahwa pegawai ke-1 membeli kayu seharga Rp. 30.000/m3, pegawai ke-2 Rp.35.000/m3, pegawai ke-3 Rp.32.000/m3. Berapa rata-rata harga kayu per meter kubik yang telah dibayar oleh perusahaan. Si A bepergian pulang pergi. Saat pergi kecepatannya 10 km/jam dan pulangnya 20 km/jam. Berapa rata-rata kecepatan pulang pergi?
Dalam postingan kali ini akan dibahas dulu untuk rata-rata hitung
Rata-rata hitung adalah rata-rata yang paling sering digunakan dalam kehidupan sehari-hari. Para guru sering membuat rata-rata nilai siswa selama satu catur wulan tertentu. Adapun untuk data tunggal, rumus dalam menghitung rata-rata dapat menggunakan tiga cara. Dalam buku ini hanya akan dibahas satu cara yaitu:

untuk data tunggal dan

Untuk data kelompok dimana i=1,2, k (k adalah banyaknya interval kelas) fi adalah frekuensi kelas ke-I dan Xi adalah nilai tengah kelas ke- i.
Misalnya kita memiliki data hasil ujian 25 orang siswa/i sejarah peradaban Islam MTs Darul Hikmah sebagai berikut:
79 63 72 82 74
36 42 67 51 88
68 73 78 77 96
67 67 48 41 57
91 45 83 71 50
Maka kita dapat menghitung rata-rata nilai siswa MTs Darul Hikmah untuk mata pelajaran Sejarah Peradaban Islam dengan menggunakan rumus di atas sebagai berikut:

jadi rata-ratanya adalah (x ̅) = 66,64
Jika data di atas kita buat dalam bentuk kelompok, maka yang pertama yang harus dilakukan adalah membuat tabel distribusi seperti dibawah ini:

Dengan menggunakan rumus di atas maka kita dapat menentukan rata-rata dengan cara:

bandingkan hasil perhitungan data kelompok dengan data tunggal!!
kita menemukan bahwa menghitung mean pada data berkelompok menghasilkan nilai yang berbeda dengan menghitung mean pada data tunggal. Aspek ramalan yang kita gunakan pada penentuan mean dengan menggunakan data berkelompok turut menentukan hasil mean yang kita temukan. Ternyata menentukan modus dengan tidak mengelompokkan data lebih tepat daripada kita mengelompokkan data terlebih dahulu. tingkat ketempatan akurasi ini dikarenakan dengan manggunakan data tunggal, maka yang kita hitung adalah data sebenarnya.
*Modus :
Modus merupakan fenomena yang paling banyak terjadi. Modus paling banyak digunakan pada penelitian kualitatif. Dalam penelitian kualitatif, hal yang paling banyak menyebabkan suatu keadaan sering di anggap penyebab keadaan tersebut. Misalnya kebanyak kecelakaan lalulintas disebabkan oleh pengemudi yang mabuk. Pengemudi yang mabuk dalam hal ini adalah “modus”. Dalam data berbentuk kuantitatif, modus sangat mudah untuk dideteksi. Dengan melihat data kita tinggal menentukan angka berapa yang paling sering muncul. Angka yang sering muncul itulah yang kita sebut dengan modus.
Pada data nilai siswa pada mata pelajaran sejarah kebudayaan Islam di atas terlihat bahwa angka yang paling sering muncul adalah 67 yang muncul sebanyak tiga kali dan tidak ada yang muncul sebanyak itu dari data yang lain. Akan tetapi pada data yang telah tersusun dalam tabel frekuensi, modus dapat di cari dengan menggunakan rumus:

Keterangan:
b = batas bawah kelas modus yaitu kelas yang memiliki frekuensi terbanyak
p = panjang kelas modus
b1 = frekuensi kelas modus dikurangi frekuensi kelas interval dengan tanda kelas yang lebih kecil sebelum tanda kelas modus
b2 = frekuensi kelas modal dikurangi frekuensi kelas interval dengan tanda kelas yang lebih besar sesudah tanda kelas modus.
Misalnya dari tabel frekuensi di atas kita dapat menghitung modusnya. Dengan memperhatikan tabel kita akan menemukan
b = 70,5
p = 10
b1 = 7 – 5 = 2
b2 = 7 – 3 = 4
Dengan memasukkan data tersebut ke dalam rumus akan kita dapatkan
Kembali kita menemukan bahwa menghitung modus pada data berkelompok berbeda dengan menghitung modus pada data tunggal. Aspek ramalan yang kita gunakan pada penentuan modus dengan menggunakan data berkelompok turut menentukan hasil modus yang kita temukan. Ternyata menentukan modus dengan tidak mengelompokkan data lebih tepat daripada kita mengelompokkan data terlebih dahulu.
Median adalah datum yang membagi data menjadi dua kelompok, 50 persen data kurang dari nilai median dan 50 persen data lebih besar dari median. Pada data tunggal, pencarian nilai median dilakukan dengan cara mengurutkan data dari nilai terkecil ke nilai terbesar. Kemudian nilai tengah data yang telah diurutkan itu merupakan nilai median.
Bagaimana menentukan nilai median dari data berkelompok? Bagaimana penurunan formula nilai median untuk data berkelompok hingga menjadi rumus sebagai berikut:
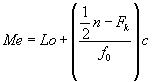
di mana:
Lo = tepi bawah dari kelas limit yang mengandung median,
Me = nilai median,
n = banyaknya data,
Fk = frekuensi kumulatif sebelum kelas yang memuat median,
f0 = frekuensi kelas yang memuat median,
c = panjang intreval kelas.
Perhatikan Tabel di Bawah ini:
| Kelas | Frekuensi | F_Kumulatif |
| 15 – 19 | 5 | 5 |
| 20 – 24 | 7 | 12 |
| 25 – 29 | 10 | 22 |
| 30 – 34 | 15 | 37 |
| 35 – 39 | 13 | 50 |
| 40 – 44 | 8 | 58 |
| 45 – 49 | 6 | 64 |
Bentuk histogram dari Tabel Di atas adalah:
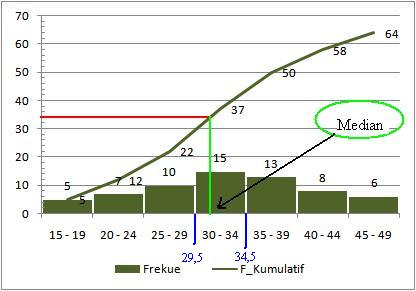
Oleh karena banyaknya data 64, maka nilai median jatuh pada data ke-32. Garis merah horizontal menunjukkan posisi data ke-32 sementara garis hijau muda vertikal menunjukkan median data berkelompok dari data di atas. Jumlah kumulatif hingga kelas limit ketiga adalah 22. Berarti, posisi median berada pada data ke-10 (32 – 22) pada kelas limit keempat. Bilangan ini diperoleh dari (n/2 – Fk).
Median data berkelompok dihitung berdasarkan interpolasi dari posisi data pada kelas limit yang mengandung median. Secara matematis, persamaannya dapat ditulis sebagai berikut.
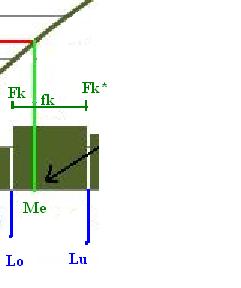
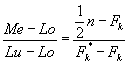
Sehingga dengan manipulasi matematik akan diperoleh persamaan:
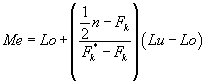
Di mana: Lu – Lo menyatakan panjang interval kelas c dan Fk* – Fk menunjukkan frekuensi kelas limit median f0. Dengan demikian, median data berkelompok yang dihasilkan sama dengan:
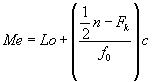
Demikian asal muasal median untuk data berkelompok. Semoga menambah khazanah perstatistikan pembaca.
